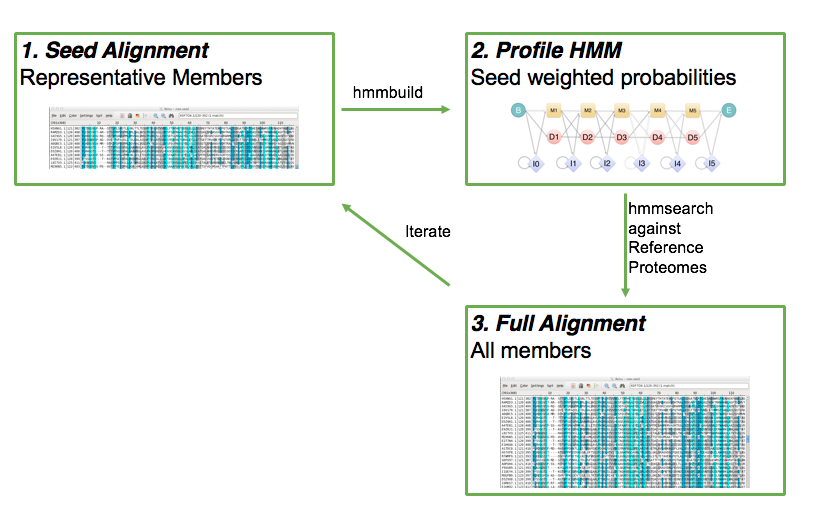
class: center, middle, inverse, title-slide .title[ # Lecture 4: Multiple alignments, motifs and logos ] .subtitle[ ## BE_22 Bioinformatics SS 21 ] .author[ ### January Weiner ] .date[ ### 2024-04-29 ] --- ## Sequence conservation & logos  --- ## What are these bits?? Visualize uncertainty (defined as Shannon entropy) about a given position using *information bits*. Entropy at position `\(i\)` describes the probability with which we can predict the outcome: `\(H_i = - \sum_{aa=1}^{20} f_{aa,i} \cdot \log_2 f_{aa,i}\)` -- For example, if at a certain position we have 100 % Ala and 0 % of other amino acids, `\(H_i = -f_{Ala,i}\cdot \log_2 f_{Ala,i} + \sum_{aa \neq Ala} f_{aa,i}\log_2 f_{aa, i} = - 1 \cdot \log_2 1 + 0 = 0\)` -- But if Ala and His are at equal frequencies, we get `\(H_i = -0.5 \log_2 0.5 - 0.5 \log_2 0.5 = - 0.5 \cdot -1 - 0.5 \cdot -1 = 1\)` -- And if all amino acids are at the same frequencies, we have `\(H_i = -20 \cdot 0.05 \cdot \log_2 0.05 \approx -20 \cdot 0.05 \cdot -4.3 = 4.3\)` --- ## What are these bits?? Bits are now defined as `\(R_i = \log_2 20 - H_i + e_n \approx 4.3 - H_i\)` (where `\(e_n\)` is correction for small sample sizes (reduces to zero for large number of sequences) -- So for all frequencies equal, `\(H_i \approx 4.3\)` and `\(R_i \approx 0\)`; for one frequency equal to 100%, `\(H_i = 0\)` and `\(R_i \approx 4.3\)`. -- This gives a scaling factor for the height of the letters: `\(bits = y_{aa,i} = f_{aa,i} \cdot R_i\)` ---  --- ## Our many hemoglobins...  --- ## Our many hemoglobins...  So, why do we need so many? `\(\rightarrow\)` example of subfunctionalization --- ## Zeta hemoglobin function .pull-left[  ] .pull-right[  ] --- ## Zeta hemoglobin function  --- ## Zeta hemoglobin function  --- ## Multiple sequence alignments   --- ## Multiple sequence alignments What is it good for?  --- ## Multiple sequence alignments * Find groups of sequences * Determine conserved regions * Conserved region: important! `\(\rightarrow\)` purifying selection * Find motifs and domains * Find common physical properties * Do changes in amino acids cause changes in physical properties? * Create profiles / HMM models for sensitive homology search * First step to phylogeny reconstruction --- The alignment clearly shows the two paralogs of hemoglobin (A and B)  --- Alignment showing physical properties of amino acids  --- We can find conserved regions / protein domains  --- ## How to score a multiple alignment Add scores from all possible pairs of sequences Score for a column `\(i\)` in a multiple sequence alignment: `$$S_i = \sum_{j=1}^{N} \sum_{k=j + 1}^{N} aa_{i,j,k}$$` Score for the full alignment: `$$S = \sum_{i=1}^L \sum_{j=1}^{N} \sum_{k=j + 1}^{N} aa_{i,j,k}$$` where `\(L\)` is the length of the alignment, `\(N\)` is the number of sequences, and `\(aa_{i,j,k}\)` denotes scores between sequences `\(j\)` and `\(k\)` in column `\(i\)`. --- ## Extending NW approach  --- ## Extending NW approach  --- ## Extending NW approach  --- ## Extending NW approach  --- ## Extending NW approach  --- ## Extending NW approach  --- ## Extending NW approach * complexity grows with each sequence in MSA * for 3 sequences, `\(O(n^3)\)`; for 4, `\(O(n^4)\)`, etc. `\(\rightarrow O(n^k)\)` * naive application completely useless * sped up with Carillo-Lipman approach, but still not scalable * not realistic for more than 4 sequences --- ## Heuristic * compromise accuracy vs speed * algorithms: * progressive algorithms * clustal[o,w] `\(O(N^2)\)` (clustalw), `\(O(N\log{N})\)` (clustalo) * kalign * stepwise improvement / genetic * MUSCLE `\(O(N^3L)\)` --- ## ClustalW progressive algorithm .pull-left[  ] .pull-right[ * Calculate pairwise similarity (distance) between each two sequences * Build a similarity matrix * Create a "guide tree" (which sequences are next to each other?) * Step-wise assembly along the tree ] --- ## Distance and score * Score is calculated by the "sum of all pairs" approach * Using an appropriate function, we can always convert a score into a distance For example, the original clustalw algorithm used the following distance function: `$$D_{i,j} \stackrel{def}{=} 1 - P_{i,j}$$` Where `\(P_{i,j}\)` is the percentage identity between sequences `\(i\)` and `\(j\)`. The reason for using this simple function was its speed. --- ## Distance and score Feng and Doolittle method (1996): * Calculate the pairwise score between two matrices using an approppriate matrix `\(S_{real}\)` * Determine "background" scoring of randomly shuffled sequences (average between several sequences, `\(S_{rand}\)` * Determine the "maximum possible" score by aligning first and second sequences to itself and determining the average, `\(S_{iden} = \frac{S_{1,1} + S_{2,2}}{2}\)` Then calculuate the normalized score: `$$S = \frac{S_{real} - S_{rand}}{S_{iden} - S_{rand}} \times 100$$` And the distance `\(D = -\log{S}\)` .footnote[Feng, Da-Fei, and Russell F. Doolittle. "[21] Progressive alignment of amino acid sequences and construction of phylogenetic trees from them." Methods in enzymology. Vol. 266. Academic Press, 1996. 368-382.] --- ## ClustalW algorithm  --- ## ClustalW algorithm  --- ## ClustalW algorithm  --- ## ClustalW algorithm  --- ## DNA/RNA sequence motifs Protein binding motifs – binding transcription factors etc.  STAT3 – member of the JAK/STAT pathway  BATF::JUN heterodimer --- ## DNA/RNA sequence motifs Examples: * Shine-Dalgarno sequence 5'-AGGAGGU-3' in the untranslated region of mRNA, complementary to a sequence in the 16S rRNA, 5'-ACCUCCU-3': .pull-left[  ] .pull-right[  ] .pull-left[ * Kozak sequence in eukaryotes (detected by scanning by the PIC, pre-initiation complex, which contains S40).  ] .pull-right[  ] ??? Lynn Dalgarno (top middle) John Shine (top left) --- * Bacteria: Shine Dalgarno seqence or leaderless transcripts (which start with ATG) * Archaea: Shine Dalgarno, Kozak, leaderless transcripts * Eukaryota: Kozak sequence --- ## Position specific scoring matrices (PSSMs) Creating a BLOSUM-like scoring system which depends on the *position* to detect motifs.  --- ## Position specific scoring matrices (PSSMs) * regulators * AT-rich upstream region * -35 box * -10 box (Pribnow box) * +1 / ATG --- ## Pribnow box (-10 box)  * Not all promoters have the same sequence * Small differences follow a statistical distribution --- Battle plan: For each of the three main regions (-35, -10 and +1) create small alignments. -- In an alignment, count the frequencies of the four nucleotides at each position and calculate scores as log-odds ratios `$$S_{nn,i} = \log\frac{f_{o,i}}{f_e}$$` Where `\(f_e\)` is the expected frequency of nucletide `\(nn\)` (given by the GC contents), `\(f_{o,i}\)` is the observed frequency at position `\(i\)`, and `\(S_{nn,i}\)` is the position-specific score. -- Then, slide the three matrices along a DNA sequence and find the position(s), where the overall score is maximal (we add the scores of the three matrices together). ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  ---  --- class:empty-slide,myinverse background-image:url(images/cute_puppy.jpg) --- # Position specific iterated BLAST (PSI-BLAST) * Find a bunch of hits with regular BLAST * run a multiple sequence alignments on selected hits * create a PSSM * get better hits * rinse and repeat ---  --- # Hidden Markov Models  --- # Hidden Markov Models